Next, consider the equilibrium of the stress element for shear stresses. Let the dimension of the square stress element be denoted by Δx and Δy, and let the thickness of the stress element in the z direction be Δz.
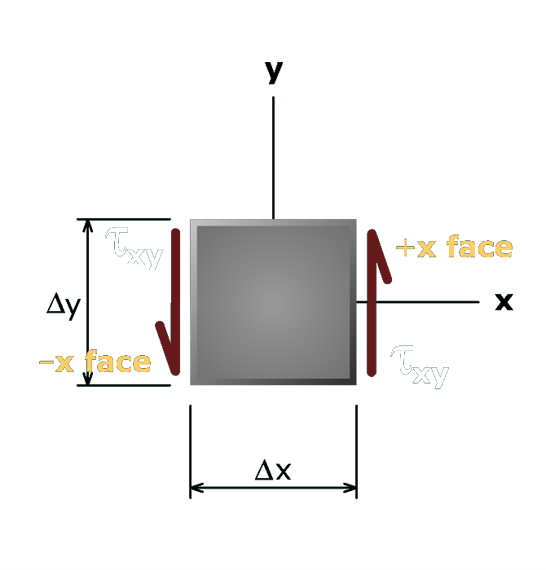
Suppose we have a positive shear stress acting in the +y direction on the +x face.
The corresponding force will be:
V = τxy Δy Δz
acting upward.
To satisfy equilibrium in the y direction, the shear stress on the –x face must act in the –y direction.
We can make a similar equilibrium argument about τyx acting on the y faces to show that shear stresses on the +y and –y faces must be equal in magnitude and opposite in direction.