Assuming that the moments and product of inertia of an area are known about orthogonal coordinate axes $\mathrm{x}$ and $\mathrm{y}$, the moments and product of inertia about new axes $\mathrm{x}\text{'}$ and $\mathrm{y}\text{'}$ may be determined from the equations:

${\mathrm{I}}_{\mathrm{x}\text{'}}=\frac{{\mathrm{I}}_{\mathrm{x}}+{\mathrm{I}}_{\mathrm{y}} }{2}+\frac{{\mathrm{I}}_{\mathrm{x}}-{\mathrm{I}}_{\mathrm{y}} }{2}\cos 2\mathrm{\theta } - {\mathrm{I}}_{\mathrm{xy}}\sin 2\mathrm{\theta }$

${\mathrm{I}}_{\mathrm{y}\text{'}}=\frac{{\mathrm{I}}_{\mathrm{x}}+{\mathrm{I}}_{\mathrm{y}} }{2}-\frac{{\mathrm{I}}_{\mathrm{x}}-{\mathrm{I}}_{\mathrm{y}} }{2}\cos 2\mathrm{\theta } + {\mathrm{I}}_{\mathrm{xy}}\sin 2\mathrm{\theta }$

${\mathrm{I}}_{\mathrm{x}\text{'}\mathrm{y}\text{'}}=\frac{{\mathrm{I}}_{\mathrm{x}}-{\mathrm{I}}_{\mathrm{y}} }{2}\sin 2\mathrm{\theta } + {\mathrm{I}}_{\mathrm{xy}}\cos 2\mathrm{\theta }$

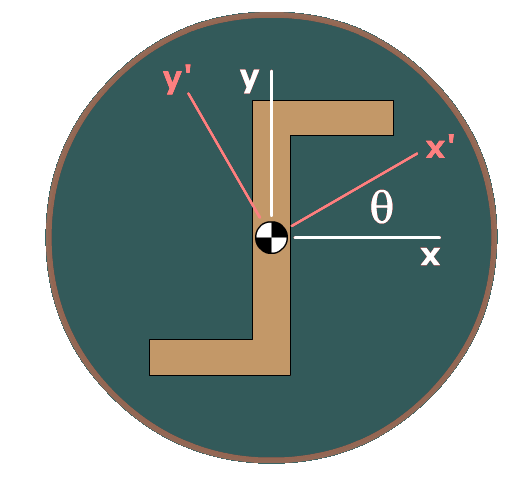
There exists one set of axes for which the moments of inertia of an area are maximum and minimum. These axes are called the principal axes of an area. The values of the maximum and minimum moments of inertia can be found from:

${\mathrm{I}}_{p1},{\mathrm{I}}_{p2}=\frac{{\mathrm{I}}_x+{\mathrm{I}}_y}{2}\pm \sqrt{{\left(\frac{{\mathrm{I}}_x-{\mathrm{I}}_y}{2}\right)}^2+{I_{xy}}^2}$