MecMovies 4.0 : M1.13: Force Based on Inclined Plane Stresses

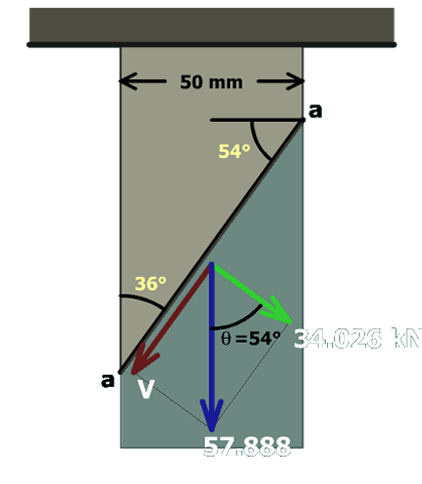
The figure shows a vertical bar of width 50 millimeters fixed to the ceiling. An inclined plane labeled a a is shown and it is at an angle of 36 degrees with respect to the vertical and 54 degrees with respect to the horizontal. The load on the inclined surface has a magnitude of 57.888 and is directed vertically downwards. This load is resolved into a vector v parallel to the inclined surface and a vector of magnitude 34.026 kilo newton perpendicular to the inclined surface and making an angle theta which equals 54 degrees with the vertical.

The angle between normal force component $N$ and the resultant axial force $P$ is equal to the angle $θ$ between the inclined plane surface $a - a$ and the surface that is perpendicular to the vertical force (i.e., the horizontal plane).

The resultant axial force $P$ is related to the normal component $N$ by the cosine function:

$\cos 54^{\circ} = \frac{N}{P} ∴ P = \frac{N}{\cos 54^{\circ}} ∴ P = \frac{34.026 kN}{0.58779} = 57.888 kN$