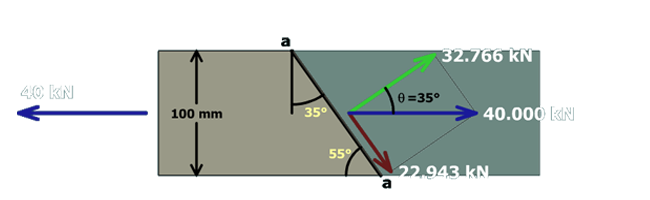
To compute the stresses acting on section , the area of the inclined plane must also be determined.
The bar height is . Use the angle to compute the length of the inclined surface:
The bar is thick; therefore, the inclined plane area is:

To compute the stresses acting on section , the area of the inclined plane must also be determined.
The bar height is . Use the angle to compute the length of the inclined surface:
The bar is thick; therefore, the inclined plane area is: