MecMovies 4.0 : M6.5: Minimum Diameter for a Solid Shaft

Manipulate the elastic torsion formula so that the unknown terms are on the left-hand side of the equation.

$τ = \frac{Tc}{J} ∴ \frac{J}{c} = \frac{T}{τ}$

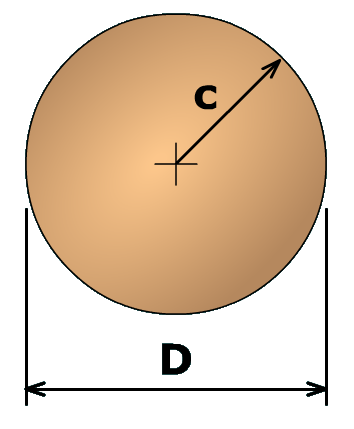
The radius $c$ can be expressed in terms of the outside diameter $D$ :

$c = \frac{D}{2}$

The polar moment of inertia $J$ for a solid circular cross section is given by:

$J = \frac{π}{32} D^{4}$

Therefore, the left-hand side of the equation above can be expressed as:

$\frac{J}{c} = \frac{{πD}^{4}}{32} \div \frac{D}{2} = \frac{π}{16} D^{3}$

The two unknown terms

c

and

J

have been expressed in terms of one variable,

D

, which makes the equation solvable.