Things to Look for In M Diagrams  
scene 7 of 12
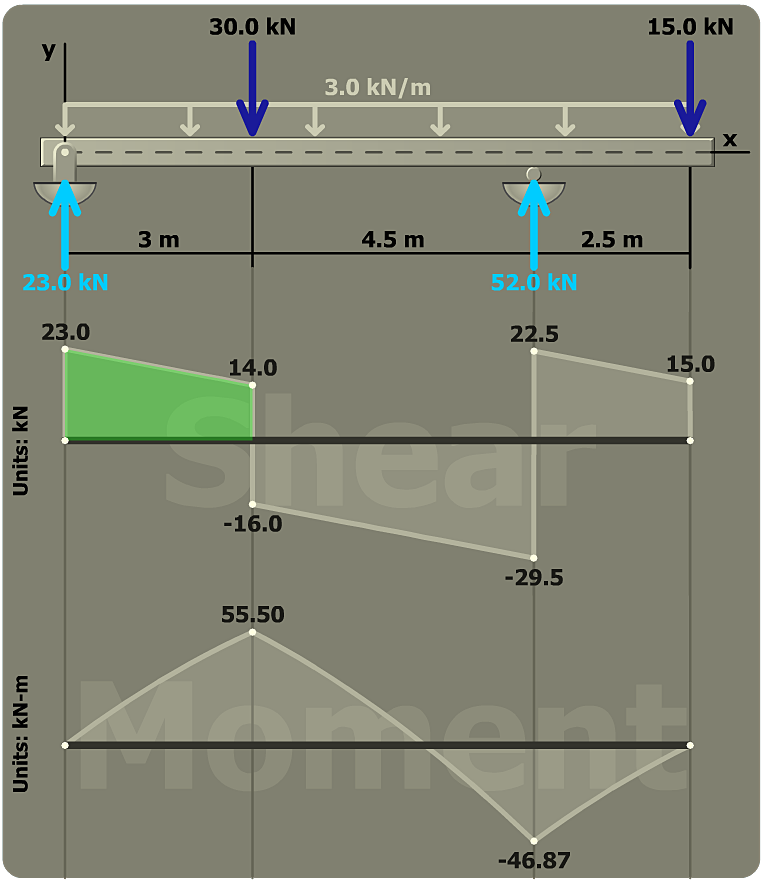
The figure shows a beam of length 10 meters with pin support at its left end and roller support at a distance of 2.5 meters from its right end. The x axis is taken along the length of the beam and the y axis is taken perpendicular to the beam at its left end. A uniform load of 3 kilo newton per meter acts throughout the length of the beam. A concentrated load of 30 kilo newtons directed vertically downwards acts 3 meters from its left end and a concentrated load of 15 kilo newtons directed vertically downwards acts on its right end. The reaction force on the pin support has a magnitude of 23 kilo newtons and is directed vertically upwards. The reaction force on the roller support has a magnitude of 52 kilo newtons directed vertically upwards. The shear force and bending moment diagrams are shown below. The shear force is in units of kilo newtons. The shear force rises from 0 to 23 on the left end, linearly decreases to 14 over a length of 3 meters, the area under this curve is highlighted, it then drops to negative 16, linearly decreases to negative 29.5 over a length of 4.5 meters, rises to 22.5, linearly decreases to 15 over a length of 2.5 meters and drops to zero at the right end of the beam. The bending moment is in units of kilo newton meter. The bending moment starts from zero on the left end, rises to 55.5 over a length of 3 meters, decreases to negative 46.87 over a length of 4.5 meters and rises to 0 over a length of 2.5 meters.

Areas under the shear diagram must be computed to construct the bending-moment diagram. Frequently, the area of a trapezoid (such as the area highlighted on the shear diagram at the left) must be determined.

While the trapezoid could be divided into a rectangle and a triangle, the following approach is much quicker:

1. Add the heights of the left and right sides of the trapezoid.

2. Divide this number by 2 to obtain the average height.

3. Multiply the average height by the base width to obtain the area.