The flexure formula defines the relationship between elastic stresses and the moment applied to the beam.

The normal stress produced in a beam by a bending moment M increases linearly as the distance from the neutral axis is increased.
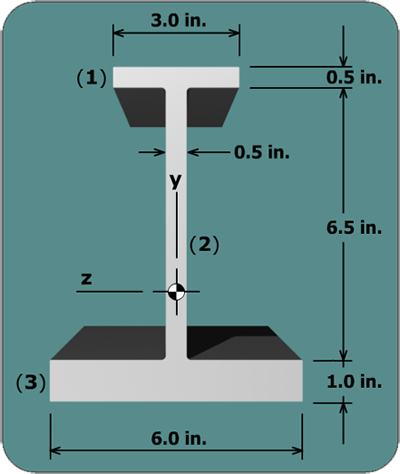
Since the beam cross section is not symmetrical about the horizontal centroidal axis (i.e., the z axis in this case), we must compute normal stresses at both the top and bottom surfaces of the cross section.