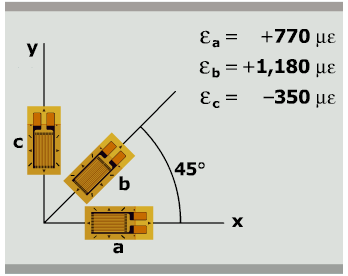
MecMovies 4.0 : M13.6: Principal Stresses from Rosette Data

In working with strain rosettes, a strain transformation equation is written for each strain gage.

$ε_{a} = ε_{x} \cos^{2} θ_{a} + ε_{y} \sin^{2} θ_{a} + γ_{xy} {sinθ}_{a} {cosθ}_{a}$
$ε_{b} = ε_{x} \cos^{2} θ_{b} + ε_{y} \sin^{2} θ_{b} + γ_{xy} {sinθ}_{b} {cosθ}_{b}$
$ε_{c} = ε_{x} \cos^{2} θ_{c} + ε_{y} \sin^{2} θ_{c} + γ_{xy} {sinθ}_{c} {cosθ}_{c}$

These three equations are solved simultaneously for the three unknowns ε_x, ε_y, and γ_xy.

Using the values for ε_x, ε_y, and γ_xy, the stresses σ_x, σ_y, and τ_xy can be determined from the generalized Hooke's Law equations:

σ_{x} = \frac{E}{(1 - ν^{2})} (ε_{x} + {νε}_{y}) σ_{y} = \frac{E}{(1 - ν^{2})} (ε_{y} + {νε}_{x}) τ_{xy} = {Gγ}_{xy}