$\sum _{}{\mathrm{M}}_{\mathrm{C}}={\mathrm{F}}_1(750 \mathrm{mm})-{\mathrm{F}}_2(300 \mathrm{mm})-\mathrm{P}(400 \mathrm{mm})=0$

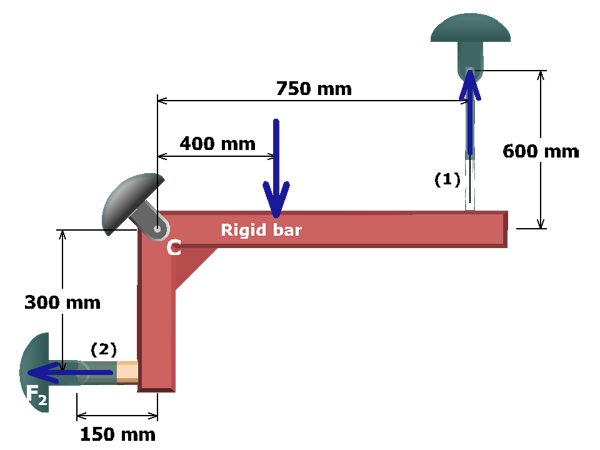
From inspection of this equation, observe that there are two unknowns: ${\mathrm{F}}_1$ and ${\mathrm{F}}_2$. While additional equilibrium equations could be written, each new equation would introduce a new unknown. Consequently, this problem cannot be solved using statics alone. This type of problem is known as statically indeterminate.