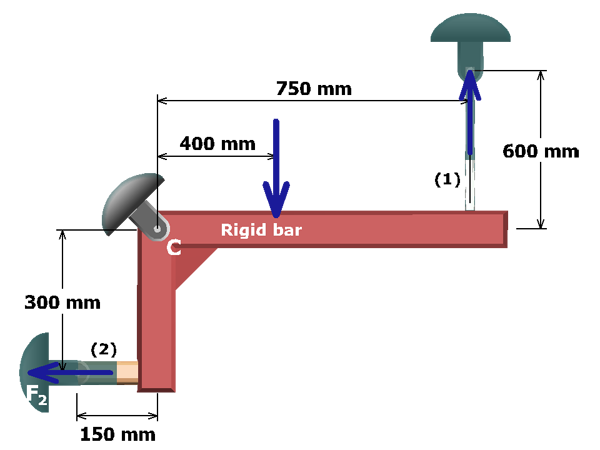
To solve for the internal forces and , a second equation involving these two unknowns must be developed. To do this, the rigid bar geometry and the deformation of the axial members will be considered.

To solve for the internal forces and , a second equation involving these two unknowns must be developed. To do this, the rigid bar geometry and the deformation of the axial members will be considered.