The procedure needed to solve this problem can be outlined as:
• Equilibrium
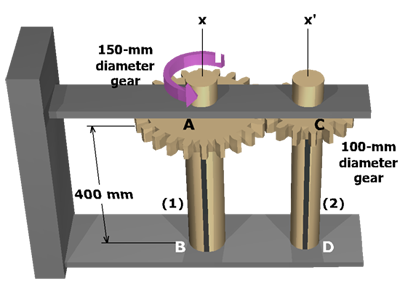
Draw one FBD of gear A and shaft (1) and a second FBD of gear C and shaft (2) to deduce the relationship of internal torques
T1 and T2 to the applied torque T.
• Geometry of deformation
From the rotation angles of gears A and C, the relationship between the twist angles in shafts (1) and (2) will be determined.
• Torque-twist relationships
The relationship between internal torque and angle of twist angle is stated for each shaft.
• Compatibility equation
The torque-twist relationships will be substituted into the geometry of deformation relationship to derive a compatibility equation expressed in terms of the internal torques T1 and T2.
Answer the questions
Once T1 and T2 are determined, the values required for this problem will be calculated.