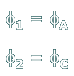
If we equate arclengths and account for the opposite rotation directions, we obtain:
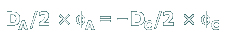
where φA and φC are gear rotation angles.
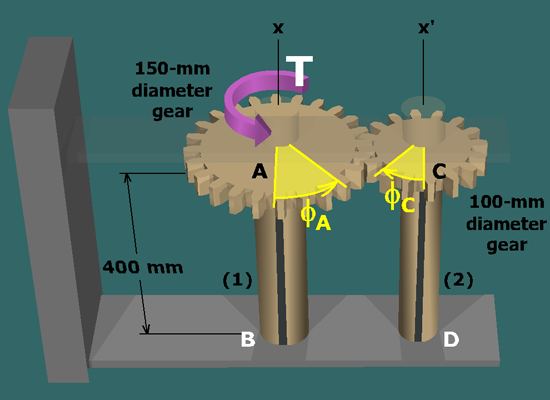
The twist angle is the difference in rotation angles at the forward and aft ends of a shaft. For shafts (1) and (2):
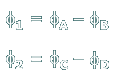
Since B and D are fixed supports, the rotation angles are zero at these points. Therefore: