Assume that member (1) controls. Substitute into the equilibrium equations and solve for and .
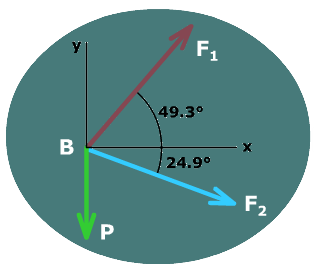
The following values are obtained from this calculation:
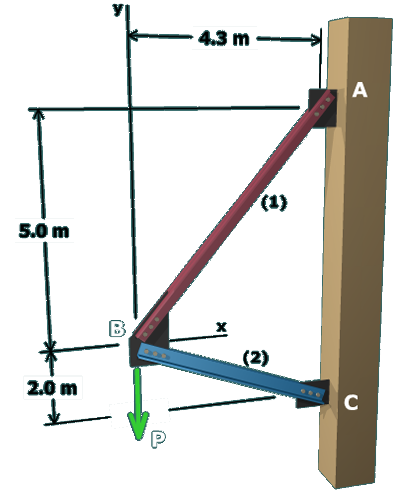
Assume that member (1) controls. Substitute into the equilibrium equations and solve for and .

The following values are obtained from this calculation:
