Solve for in terms of :
Substitute into to determine in terms of the unknown :
and backsubstitute to determine in terms of the :
The unknown can now be stated in terms of the two member forces:
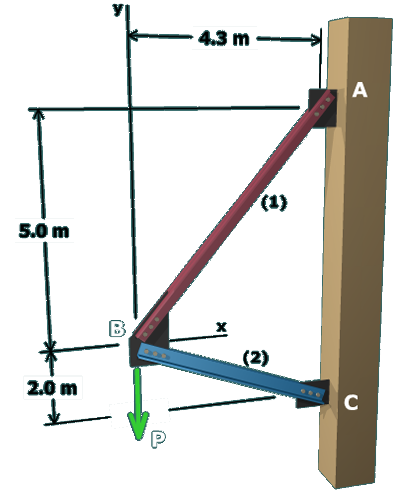
Solve for in terms of :
Substitute into to determine in terms of the unknown :
and backsubstitute to determine in terms of the :
The unknown can now be stated in terms of the two member forces:
