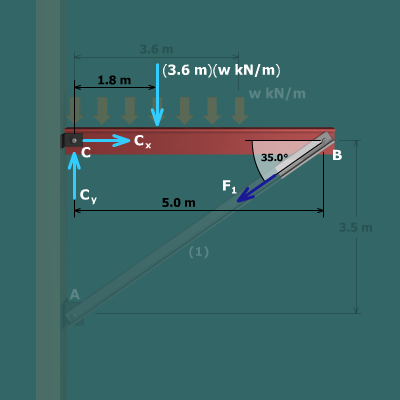
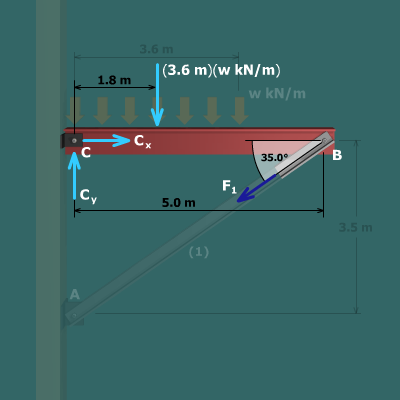
Consider axial member . The limiting stress in this member is specified as , and a factor of safety of is required. The allowable normal stress for member is therefore:
Based on this stress, the allowable force magnitude for member is:
In the preceding scene, it was shown that the force in member could be expressed in terms of as:
Equate these two expressions and solve for .
Since only the magnitude of is desired, consider the absolute value of .