MecMovies 4.0 : M6.8: Maximum Torque Based on Twist Angle

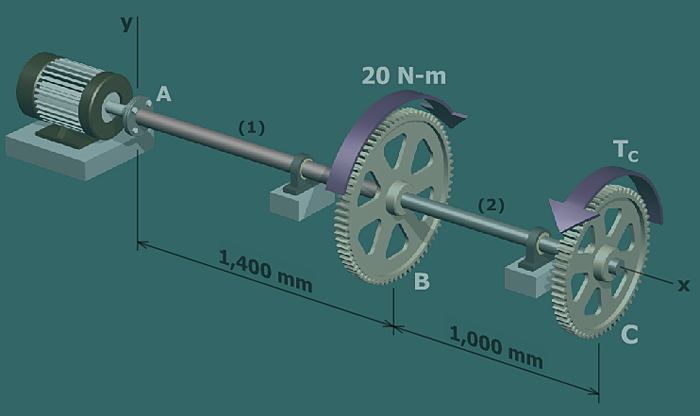
Diagram shows a shaft A B C containing two gears at B and C which is connected to a motor A where the torques of 20 Newton meter and T subscript c is applied on B and C and the distance A B is 1400 millimeters and BC is 1000 millimeters. The x axis is taken along the axis of the gears and the y axis is taken along the motor support at A and perpendicular to the x axis.

• Equilibrium
Cut free-body diagrams $(FBD)$ through shafts $(1)$ and $(2)$ to derive equations for internal torques $T_{1}$ and $T_{2}$ in terms of the unknown torque $T_{C}$ .

• Torque-twist relationships
Express the relationship between internal torque and angle of twist for each shaft.

• Geometry of deformation
The angle of rotation at $C$ will be the sum of the twist angles in shafts $(1)$ and $(2)$ .

• Equation for rotation angle at $C$
Substitute the torque-twist relationships into the geometry of deformation equation to derive an expression for the rotation angle at $C$ .

• Express in terms of $T_{C}$
Substitute the expressions for $T_{1}$ and $T_{2}$ derived from equilibrium into the equation for the rotation angle at $C$ .

• Solve for $T_{C}$
Manipulate this equation and solve for $T_{C}$ .