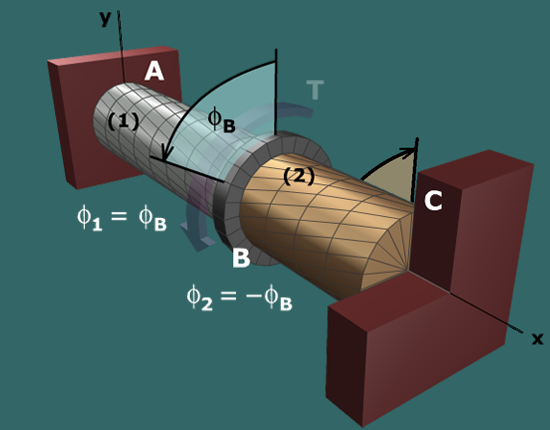
The angle of twist in shaft and expressed in terms of rotation angles are therefore:
Since the rotation angle at is known (i.e., ), the above relations can be combined with the torque-twist relationships...
...to compute the internal torques and in the stainless steel and bronze shafts. Once these internal torques are known, the torque can be computed from equilibrium and the shear stress in each shaft can be calculated with the torsion formula.