This allows the shear strain to be written as:

${\mathrm{\gamma }}_{\max }=\frac{{\displaystyle \mathrm{c} \mathrm{d\varphi }}}{{\displaystyle \mathrm{dx}}}$

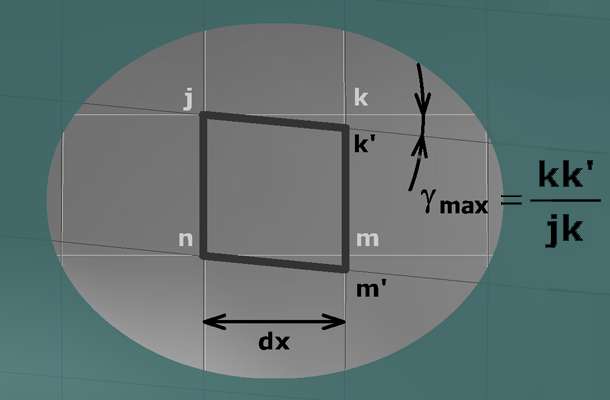
For the special case of pure torsion, the rate of twist $\mathrm{d\varphi }/\mathrm{dx}$ is constant and equal to the total angle of twist divided by the shaft length $\mathrm{L}$. Therefore, the maximum shear strain for pure torsion can be expressed as:

${\mathrm{\gamma }}_{\max }=\frac{\mathrm{c\varphi }}{\mathrm{L}}$