MecMovies 4.0 : M6.21: Maximum Torque for Composite Shaft

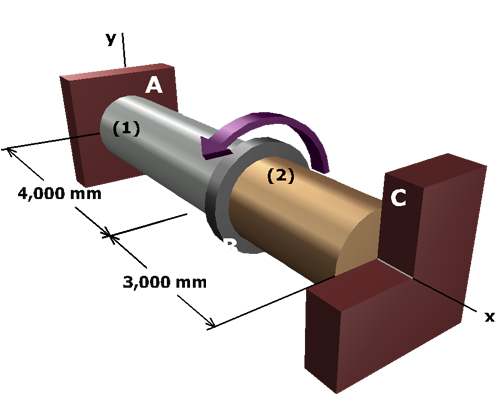
Diagram shows an aluminum shaft A B with a support at A, marked 1 of length 4,000 millimeters and a brass shaft B C with a support at C, marked 2 of length 3,000 millimeters with a flange in between at B. The shafts are centered on the x axis. A torque T is applied at B.

$\frac{τ_{1} L_{1}}{c_{1} G_{1}} = - \frac{τ_{2} L_{2}}{c_{2} G_{2}}$

Let's assume that shaft $(1)$ controls. We will assume that the shear stress in shaft $(1)$ is equal to its $90 MPa$ allowable stress.

Based on this assumption, the shear stress in shaft $(2)$ must be:

$τ_{2} = - (\frac{c_{2}}{c_{1}}) (\frac{G_{2}}{G_{1}}) (\frac{L_{1}}{L_{2}}) τ_{1} = - (\frac{40 mm}{40 mm}) (\frac{38 GPa}{76 GPa}) (\frac{4, 000 mm}{3, 000 mm}) (90 MPa) = - 60 MPa$

Since the $60 MPa$ shear stress is greater than the $50 MPa$ allowable shear stress for shaft $(2)$ , our initial assumption is incorrect. Shaft $(2)$ will actually control the capacity of the composite shaft. The shear stress magnitude in shaft $(2)$ will equal its $50 MPa$ allowable stress.